1. 문제 유형
안녕하세요. 문제 유형은 기하학이었습니다. 두 선분이 교차하는지 판별하는 문제였습니다. 이는 외적계산을 통해 방향을 판별해 주는 CCW 알고리즘을 사용해 풀이할 수 있습니다. 한 선분을 이루는 두 점과 다른 선분의 각 점에 대해서 CCW 결과가 서로 반대 방향인 경우 두 선분이 교차한다고 할 수 있습니다. 여기서 주의할 점은 한 선분의 한 점이 다른 선분이 이루는 직선 위에 있을 때를 포함해야 하는가를 판단해봐야 합니다.
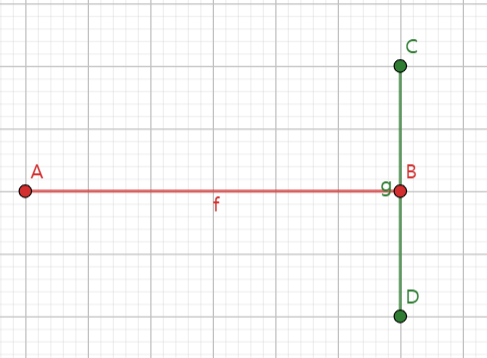
이 경우, 선분 CD에 대해서 점 A, B에 대해서 CCW를 돌리게되면 점 A는 시계 방향이므로 1이 반환되며, 점 B는 한 직선 위에 있으므로 0이 반환됩니다. 따라서 이 경우 예외 처리를 따로 해줘야 합니다. 하지만 이 경우 항상 피지가 4 등분되지 않을 가능성이 있습니다. 피자가 삼각형이라고 한다면, A, C, D가 삼각형의 꼭짓점이라고 한다면 피자는 2 등분이 됩니다.
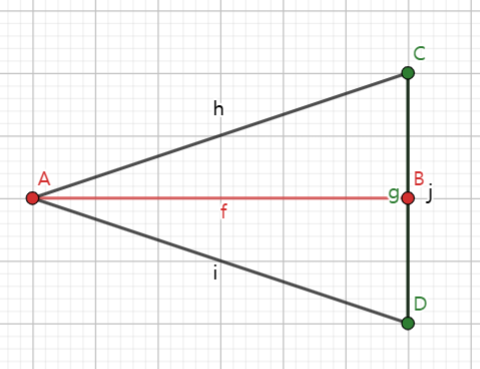
따라서, CCW 연산 결과가 0일 때, 교차하는지 예외 처리를 따로 할 필요 없이 CCW의 두 결과의 곱이 -1인지 검사만 진행하면 됩니다.
2. 코드
#include <bits/stdc++.h>
using namespace std;
typedef long long ll; typedef unsigned long long ull; typedef pair<int,int> pi; typedef pair<ll, ll> pl;
typedef tuple<int, int, int> ti; typedef tuple<ll, ll, ll> tl; typedef vector<int> vi; typedef vector<ll> vl;
typedef vector<pi> vpi; typedef vector<pl> vpl; typedef vector<ti> vti; typedef vector<tl> vtl;
typedef vector<string> vs; typedef vector<bool> vb; typedef queue<int> qi; typedef queue<ll> ql;
typedef queue<pi> qpi; typedef queue<pl> qpl; typedef queue<ti> qti; typedef queue<tl> qtl;
#define fastio(x, y) cin.tie((x))->sync_with_stdio((y))
#define X first
#define Y second
#define pb push_back
#define sz(x) (int((x).size()))
#define all(x) (x).begin(), (x).end()
#define rall(x) (x).rbegin(), (x).rend()
const char nl = '\n';
template<typename T>
class Point{
private:
T x, y;
public:
Point() {}
Point(T x, T y): x(x), y(y) { }
int ccw(const Point<T> &a, const Point<T> &b) {
T cross = (x * a.y + a.x * b.y + b.x * y) - (a.x * y + x * b.y + b.x * a.y);
if(!cross) return 0;
return (cross < 0 ? -1 : 1);
}
bool operator<=(const Point<T> &other) const {
return this -> x < other.x || (this -> x == other.x && this -> y <= other.y);
}
};
template<typename T>
class Line{
private:
Point<T> a;
Point<T> b;
bool is_inner(const Point<T> &c) {
return a <= c && c <= b;
}
public:
Line() {}
Line(T ax, T ay, T bx, T by): a(ax, ay), b(bx, by) {
if(b <= a) {
swap(a, b);
}
}
int ccw(Point<T> c) {
return a.ccw(b, c);
}
bool is_intersection(Line other) {
T this_cross = 1, other_cross = 1;
for(int i = 0; i < 4; i++) {
T cur = (i < 2 ? ccw(i ? other.b : other.a) : other.ccw(i == 2 ? a : b));
// if(!cur && (i < 2 ? is_inner(i ? other.b : other.a) : other.is_inner(i == 2 ? a : b))) return 1;
(i < 2 ? this_cross : other_cross) *= cur;
}
return (this_cross < 0 && other_cross < 0);
}
};
int main() {
fastio(nullptr, false);
Line<int> a, b;
for(int i = 0; i < 2; i++) {
int sx, sy, ex, ey;
cin >> sx >> sy >> ex >> ey;
(i ? b : a) = Line<int>(sx, sy, ex, ey);
}
cout << a.is_intersection(b);
}
3. 제출 결과
'알고리즘 > 백준' 카테고리의 다른 글
| 백준 9470번 Strahler 순서[C++] (0) | 2025.01.08 |
|---|---|
| 백준 16500번 문자열판별[C++] (0) | 2025.01.07 |
| 백준 2229번 조 짜기[C++] (0) | 2025.01.05 |
| 백준 5569번 출근 경로[C++] (0) | 2025.01.04 |
| 백준 1041번 주사위[C++] (0) | 2025.01.03 |
