글을 작성하는 이유는 세그먼트-트리 문제가 나올 때마다 구현부를 기억이 안나기도하고 제대로 코드를 이해하기 위해서 작성합니다. 아래에는 입력으로 주어지는 배열의 구간합을 구하는 로직을 세그먼트-트리로 구현한 것입니다.
1. 트리 구성하기
// 입력으로 주어지는 배열을 트리 리프에 채우기
for(int i = 0; i < n; i++) cin >> tree[i+n];
// 내부 노드에 값 할당하기
for(int i = n-1; i > 0; --i) tree[i] = tree[i<<1] + tree[i<<1|1];


2. 배열의 값이 갱신되었을 때 세그먼트-트리 갱신하기
배열에 값이 변경되었다면 세그먼트-트리 또한 변경된 배열에 맞추어 갱신해야 함.
// 배열의 p번째 값을 val로 갱신했을 때,
// 세그먼트-트리 재갱신
void update(int p, ll val){
p += n; // 인덱스 p값을 트리의 리프 노드 인덱스로 변환
tree[p] = val; // 트리의 리프값 변경(배열값이 갱신)
for(int i = p; i > 0; i >>= 1) tree[i>>1] = tree[i] + tree[i^1]; // 트리 재갱신
}

비트연산자 ^ : 0^0 = 0, 0^1 = 1, 1^0 = 1, 1^1 = 0 임 홀수면 -1 짝수면 +1


이렇게 배열의 p 번째 값이 val로 갱신되었을 때, 위 코드를 통해 루트까지 변경된 배열값에 대한 구간합을 재갱신할 수 있다.
3. 구간이 주어졌을 때, 배열의 구간합을 구하는 로직
ll query(int l, int r){
ll ret{}; // 반환값
for( l += n, r += n; l < r; l >>= 1, r >>= 1){
if(l&1) ret += tree[l++];
if(r&1) ret += tree[--r];
}
return ret;
}
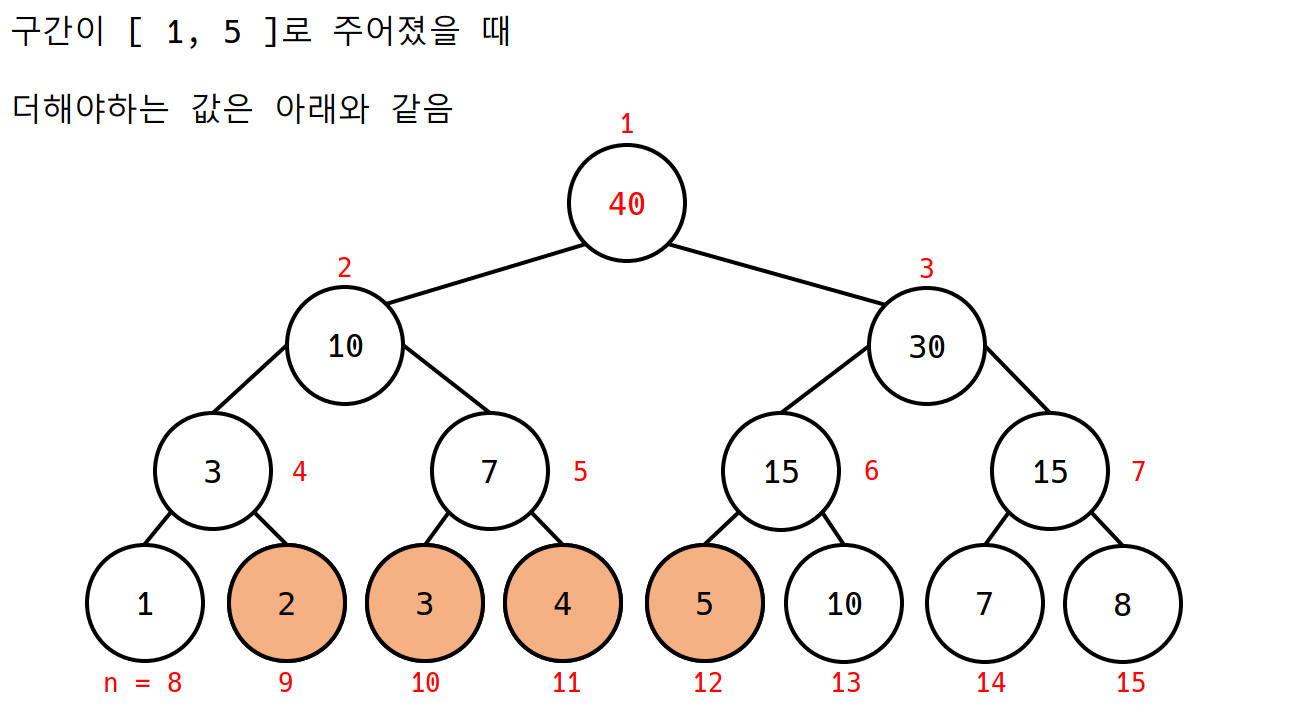


왼쪽 구간이 짝수일 때, 자신의 형제 노드인 홀수 부분도 더해야 하니 부모 노드로 이동
왼쪽 구간이 홀수일 때, 자신의 형제 노드인 짝수 부분은 이미 더했거나 더하면 안 되니 홀수 부분만 더해주고, 오른쪽으로 점프하는 듯 ( 여기서 index = 9에서 5로 점프했듯이 )
오른쪽 구간이 홀수일 때, 자신은 이미 더해졌거나 더해지면 안되므로 짝수 부분을 더하고 부모로 이동
오른쪽 구간이 짝수일 때, 자신은 이미 더해진 경우이므로 부모 노드로만 이동
혼자 생각해 봤을 때, 이런 방식으로 구동하는 코드인 것 같음 실제로 여러 시나리오를 돌려보면 이상이 없음.
코드만 보면 이해안되지만 그림을 준비하고 구간을 여러 개 직접 지정해서 움직여보면 납득이 감.
4. 구현부
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int n, m, k;
ll tree[2'000'005];
void update(int p, ll val){
p += n;
tree[p] = val;
for(int i = p; i > 0; i >>= 1) tree[i>>1] = tree[i] + tree[i^1];
}
ll query(int l, int r){
ll ret{}; // 반환값
for( l += n, r += n; l < r; l >>= 1, r >>= 1){
if(l&1) ret += tree[l++];
if(r&1) ret += tree[--r];
}
return ret;
}
int main(){
cin.tie(nullptr)->sync_with_stdio(false);
cin >> n >> m >> k;
for(int i = 0; i < n; i++) cin >> tree[i+n];
for(int i = n-1; i > 0; --i) tree[i] = tree[i<<1] + tree[i<<1|1];
}
또는 클래스로 템플릿을 만들어서 사용
template<typename T>
class SegmentTree{
private:
T *Tree;
int N;
public:
SegmentTree(vector<T> &A){
N = A.size();
Tree = new T[N * 2];
for(int i = 0; i < N; i++) Tree[N+i] = A[i];
for(int i = N-1; i > 0; --i) Tree[i] = Tree[i<<1] + Tree[i<<1 | 1];
}
~SegmentTree(){ delete [] Tree; }
void update(int p, T value){
Tree[p+N] = value;
p = p + N;
for(int i = p; i > 1; i >>= 1) Tree[i>>1] = Tree[i]+Tree[i^1];
}
T sum(int l, int r){
T ret{};
for( l += N, r += N; l < r; l >>= 1, r >>= 1){
if(l&1) ret += Tree[l++];
if(r&1) ret += Tree[--r];
}
return ret;
}
};
// vector<long long> a{1, 2, 3, 4, 5, 6, 7, 8, 9};
// SegmentTree<long long> st(a);
'알고리즘 > 알고리즘 공부' 카테고리의 다른 글
| 느리게 갱신되는 구간합 세그먼트 트리 비재귀 템플릿(SegmentTree With Lazy Propagation Template) (0) | 2024.12.31 |
|---|---|
| 구간 합 세그먼트 트리 템플릿(SegmentTree Template) [C++] (0) | 2024.12.31 |
| CCW Template (0) | 2024.12.29 |
| 벨만-포드 알고리즘(Bellman-Ford Algorithm) (0) | 2024.08.04 |
